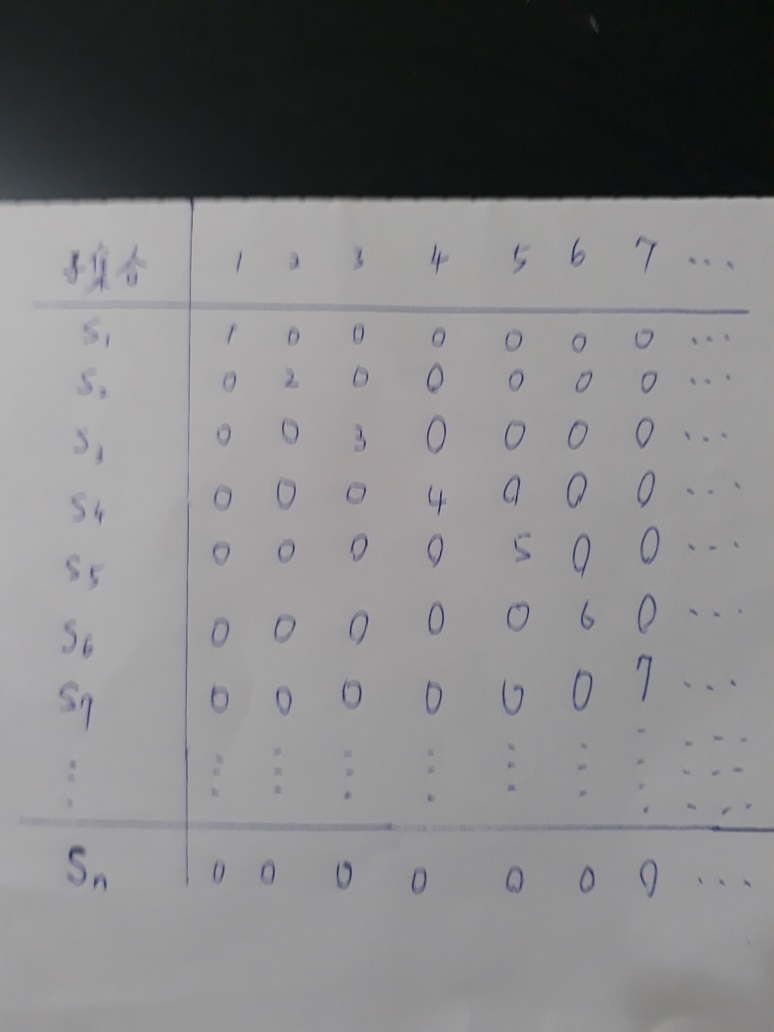
如圖

上邊是一個自然數集合

左邊是它的子集合

經過有序排列

子集合S1序數1的元素就會是1

S2序數2的元素就會是2

S3序數3的元素就會是3

…

Sk序數k的元素就會是k

假設有一個Sn

如果Sk序數k的元素不是0

那麼Sn序數n的元素是0

如果Sk序數k的元素是0

那麼Sn序數n的元素是任意自然數

這種證明過程

就是驚世駭俗的康托爾對角線證明法

而哥以上的證明過程

只是為了強調一點

就是

Sn是0集合

如圖

假設下的子集合Sn每個元素皆為0

是不是就是空集合

得出結論

假設下的Sn子集合

康托爾的說法有著邏輯問題

而哥藉以上證明

證明

假設下的Sn子集合

不是空集合

就是不存在

一舉挑戰了集合論公理

及無情地對康托爾提出質疑

連帶地

順便也證明了連續統假說